
تصویری: چگونه می توان رأس سهمی افقی را پیدا کرد؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
اگر یک سهمی دارد افقی محور، فرم استاندارد معادله سهمی این است: (y -k)2 = 4p(x - h)، که در آن p≠ 0. The راس از این سهمی در (h، k) است. تمرکز روی (h + p, k) است. Thedirectrix خط x = h - p است.
خوب، چگونه راس و جهت یک سهمی را پیدا می کنید؟
فرم استاندارد (x - h) است.2 = 4p (y - k)، که در آن تمرکز (h، k + p) و the است directrix y = k - p است. اگر سهمی به گونه ای چرخانده شده است که راس (h، k) است و محور تقارن آن موازی با محور x است، دارای یک معادله از (y - k)2 = 4p (x -h)، که در آن تمرکز (h + p, k) و the است directrix x = h - p است.
علاوه بر این، معادله سهمی جانبی چیست؟ شکل "عمومی" الف معادله سهمی همان چیزی است که به آن عادت کرده اید، y = تبر2 + bx + c - مگر اینکه درجه دوم " به پهلو "، در این صورت معادله چیزی شبیه x = ay به نظر می رسد2 + توسط +c.
خوب، چگونه راس یک معادله سهمی را پیدا می کنید؟
این نقطه، که در آن سهمی تغییر جهت می دهد، به نام راس اگر درجه دوم به شکل y = a(x – h) نوشته شود.2 + k، سپس the راس نقطه (h, k) است. این منطقی است، اگر به آن فکر کنید. قسمت مربعی همیشه مثبت است (برای سمت راست به بالا سهمی ) مگر اینکه صفر باشد.
راس سهمی برای چه مقدار p است؟
مطلق مقدار p فاصله بین راس و فوکوس و فاصله بین راس و دایرکتوریکس (علامت روشن است پ به من می گوید که از کدام راه سهمی از آنجایی که فوکوس و جهت دو واحد از هم فاصله دارند، پس این فاصله باید یک واحد باشد، بنابراین | پ | = 1.
توصیه شده:
چگونه می توان سرعت متوسط را با دو سرعت پیدا کرد؟
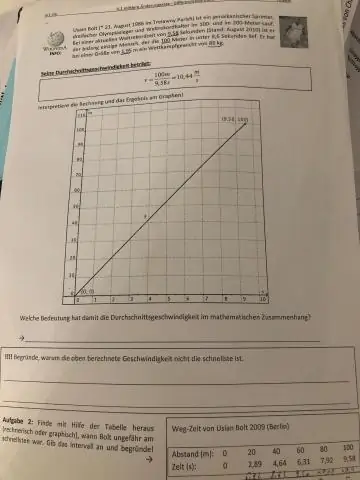
برای بدست آوردن میانگین، مجموع سرعت اولیه و نهایی بر 2 تقسیم می شود. ماشین حساب سرعت متوسط از فرمولی استفاده می کند که نشان می دهد سرعت متوسط (v) برابر با مجموع سرعت نهایی (v) و سرعت اولیه (u) تقسیم بر 2 است
چگونه می توان زوایای قاعده ذوزنقه متساوی الساقین را پیدا کرد؟

قاعده های (بالا و پایین) یک همساحلی منقطع موازی هستند. اضلاع مخالف یک همسان و غیره با طول یکسان (همگون) هستند. زوایای دو طرف پایه ها به اندازه/اندازه یکسان هستند (متجانس)
چگونه می توان سطح یک جامد را پیدا کرد؟
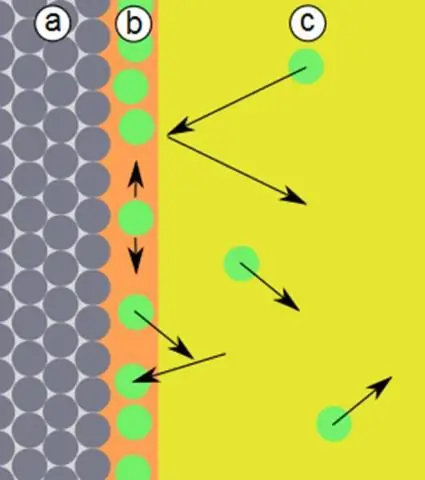
برای یافتن سطح یک منشور (یا هر جامد هندسی دیگری) جامد را مانند یک جعبه کارتن باز می کنیم و آن را صاف می کنیم تا تمام اشکال هندسی موجود را پیدا کنیم. برای یافتن حجم یک منشور (مهم نیست مستطیل یا مثلث باشد) مساحت پایه را که مساحت پایه B نامیده می شود در ارتفاع h ضرب می کنیم
چگونه می توان یک مخروط سهمی را ترسیم کرد؟
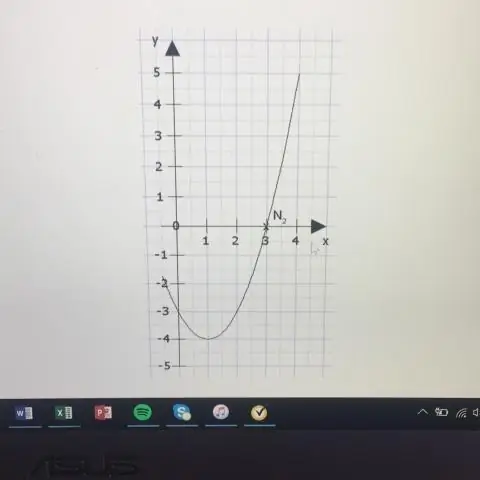
جهت یابی خط y = k - p است. محور خط x = h است. اگر p > 0، سهمی به سمت بالا باز می شود و اگر p < 0، سهمی به سمت پایین باز می شود. اگر سهمی دارای محور افقی باشد، شکل استاندارد معادله سهمی به این صورت است: (y - k)2 = 4p(x - h)، که در آن p≠ 0
چگونه می توان یک قسمت مخروطی سهمی را ساخت؟
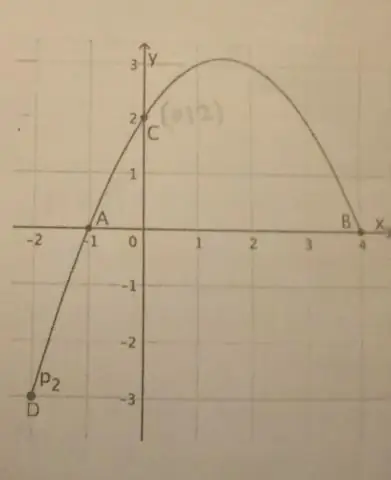
اگر یک سهمی دارای محور عمودی باشد، شکل استاندارد معادله سهمی به این صورت است: (x - h)2 = 4p(y - k)، که در آن p≠ 0. راس این سهمی در (h, k) است. تمرکز روی (h, k + p) است. جهت یابی خط y = k - p است
