
تصویری: چگونه می توان زوایای قاعده ذوزنقه متساوی الساقین را پیدا کرد؟
2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
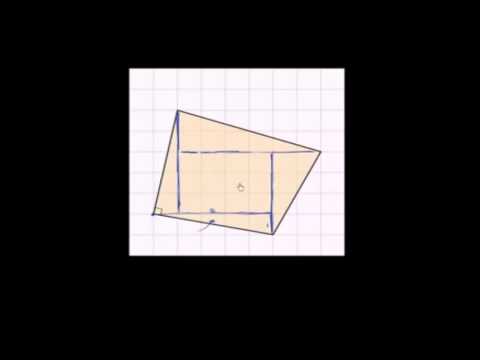
این پایه ها (بالا و پایین) یک ایزواسکلستروپوزوئید موازی هستند. طرف مقابل یک ایزواسکلستروپوزوئید طول یکسان (همسان) هستند. این زاویه یک طرف پایه ها اندازه/اندازه یکسان (همسان) هستند.
با توجه به این موضوع، آیا زوایای قاعده ذوزنقه متساوی الساقین برابر است؟
این زوایای پایه ( زاویه بین اضلاع غیر موازی و اضلاع موازی تشکیل می شود برابر در یک ذوزنقه متساوی الساقین . مورب های یک ایزواسکلستروپوزوئید هستند برابر در طول. جمع مخالف زاویه در یک ذوزنقه متساوی الساقین 180 درجه است.
دوم اینکه چگونه ذوزنقه متساوی الساقین را اثبات می کنید؟ قضیه: اگر یک چهارضلعی (با یک مجموعه اضلاع متوازی) یک باشد ذوزنقه متساوی الساقین ، پاهای آن متجانس هستند. قضیه: (مقابله) اگر a ذوزنقه ای دارای پاهای متجانس است، isan ذوزنقه متساوی الساقین . قضیه: اگر یک چهارضلعی یک باشد ذوزنقه متساوی الساقین ، قطرها همخوان هستند.
همچنین بدانید ذوزنقه متساوی الساقین چه خواصی دارد؟
چند ضلعی محدب چرخه ای
چگونه زاویه گم شده را پیدا می کنید؟
برای تعیین اندازه گیری مجهول زاویه ، حتماً از مجموع 180 درجه استفاده کنید. اگر دو زاویه داده شده، آنها را با هم جمع کرده و سپس از 180 درجه کم کنید. اگر دو زاویه یکسان و مجهول هستند، معلوم را کم کنید زاویه از 180 درجه و سپس بر 2 تقسیم کنید.
توصیه شده:
چگونه می توان سرعت متوسط را با دو سرعت پیدا کرد؟
برای بدست آوردن میانگین، مجموع سرعت اولیه و نهایی بر 2 تقسیم می شود. ماشین حساب سرعت متوسط از فرمولی استفاده می کند که نشان می دهد سرعت متوسط (v) برابر با مجموع سرعت نهایی (v) و سرعت اولیه (u) تقسیم بر 2 است
آیا زوایای قاعده در مثلث قائم الزاویه همیشه 45 است؟

در مثلث قائم الزاویه متساوی الساقین، اضلاع مساوی زاویه قائمه را می سازند. توجه داشته باشید که چون مثلث قائم الزاویه متساوی الساقین است، پس زوایای قاعده برابر هستند. (قضیه 3.) بنابراین هر یک از آن زاویه های تند 45 درجه است
آیا زوایای قاعده ذوزنقه متساوی الساقین همسو هستند؟

پایه (بالا و پایین) ذوزنقه متساوی الساقین موازی است. اضلاع مخالف ذوزنقه متساوی الساقین به یک اندازه (همسان) هستند. زوایای دو طرف پایه ها به یک اندازه / اندازه هستند (همخوان)
آیا مثلث های متساوی الساقین دارای دو زاویه متجانس هستند؟

وقتی مثلثی دو ضلع متجانس داشته باشد به آن مثلث متساوی الساقین می گویند. زوایای مقابل دو ضلع با طول یکسان متجانس هستند. به مثلثی که هیچ ضلع یا زاویه ای متجانس نباشد، مثلث اسکلن می گویند
چگونه می توان زوایای متوازی الاضلاع را پیدا کرد؟

خواص متوازی الاضلاع اضلاع مقابل همگن هستند (AB = DC). فرشتگان مقابل همسان هستند (D = B). زوایای متوالی مکمل هستند (A + D = 180 درجه). اگر یک زاویه راست باشد، پس همه زوایا راست هستند. قطرهای متوازی الاضلاع یکدیگر را نصف می کنند. هر مورب متوازی الاضلاع آن را به دو مثلث متوازن جدا می کند
