
تصویری: چگونه طول یک بخش از یک دایره را پیدا کنید؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
یک زاویه مرکزی که توسط یک قوس اصلی فرو رفته است، اندازه ای بزرگتر از 180 درجه دارد. قوس طول از فرمول برای یافتن استفاده می شود طول از یک قوس الف دایره ; l=rθ l = r θ، که θ بر حسب رادیان است. بخش مساحت A=12θr2 A = 1 2 θr 2 یافت می شود که θ بر حسب رادیان است.
به این ترتیب، چگونه طول یک سکتور را پیدا می کنید؟
به طول قوس را پیدا کنید ، با تقسیم کردن شروع کنید قوس زاویه مرکزی بر حسب درجه در 360. سپس آن عدد را در شعاع دایره ضرب کنید. در نهایت، آن عدد را در 2 × پی ضرب کنید طول قوس را پیدا کنید . اگر می خواهید یاد بگیرید نحوه محاسبه طول قوس در رادیان، به خواندن مقاله ادامه دهید!
پس از آن، سؤال این است که چگونه طول یک کمان را در یک دایره پیدا کنید؟ آ دایره دور تا دور 360 درجه است. بنابراین، اگر یک را تقسیم کنید قوس درجه را با 360 درجه اندازه گیری کنید، شما پیدا کردن کسری از دایره محیطی که قوس را تشکیل می دهد. سپس اگر عدد را ضرب کنید طول تمام راه در اطراف دایره ( دایره محیط) با آن کسری، مقدار را دریافت می کنید طول در طول قوس.
علاوه بر این، فرمول مساحت یک بخش از یک دایره چیست؟
این مساحت یک بخش از دایره ½ r² ∅ است، که r شعاع و ∅ زاویه بر حسب رادیان است که توسط کمان در مرکز دایره . بنابراین در نمودار زیر، سایهدار است حوزه برابر با ½ r² ∅ است.
چگونه یک بخش را محاسبه می کنید؟
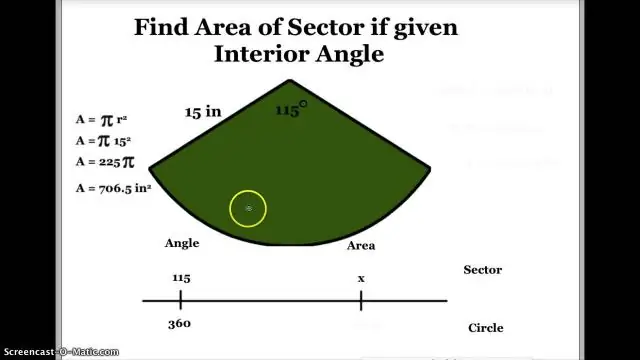
به محاسبه مساحت a بخش ، با پیدا کردن زاویه مرکزی شروع کنید بخش و آن را بر 360 تقسیم کنید. سپس شعاع یا طول یکی از خطوط را بگیرید، آن را مربع کنید و در 3.14 ضرب کنید. سپس دو عدد را ضرب کنید تا مساحت آن بدست آید بخش.
توصیه شده:
چگونه زاویه مرکزی را با توجه به مساحت و شعاع یک بخش پیدا می کنید؟

تعیین زاویه مرکزی از ناحیه بخش (πr2) × (زاویه مرکزی بر حسب درجه ÷ 360 درجه) = مساحت بخش. اگر زاویه مرکزی بر حسب رادیان اندازه گیری شود، فرمول به جای آن به صورت زیر در می آید: مساحت بخش = r2 × (زاویه مرکزی بر حسب رادیان ÷ 2). (θ ÷ 360 درجه) × πr2. (52.3 ÷ 100π) × 360. (52.3 ÷ 314) × 360
چگونه محیط دایره را پیدا می کنید؟

محیط = π x قطر دایره (ضریب پی در قطر دایره). به سادگی محیط را بر π و طول قطر را خواهید داشت. قطر فقط شعاع دو است، پس قطر را بر دو تقسیم کنید و شعاع دایره را خواهید داشت
چگونه طول قوس و مساحت بخش را پیدا می کنید؟

یک زاویه مرکزی که توسط یک قوس اصلی فرو رفته است، اندازه ای بزرگتر از 180 درجه دارد. از فرمول طول قوس برای یافتن طول قوس یک دایره استفاده می شود. l=rθ l = r &تتا؛، جایی که &تتا; بر حسب رادیان است ناحیه بخش یافت می شود A=12θr2 A = 1 2 θ r 2، جایی که θ بر حسب رادیان است
چگونه می توان زاویه یک بخش را در نمودار دایره ای پیدا کرد؟
1 پاسخ در هر بخش، 3 قسمت وجود دارد که باید در نظر گرفته شود: طول قوس کسری از محیط است. مساحت این بخش کسری از کل مساحت است. این زاویه کسری از 360 درجه است اگر بخش 20٪ نمودار دایره ای باشد، هر یک از این قسمت ها 20٪ از کل است. 20% × 360 درجه 20100 × 360 = 72 درجه
چگونه بخش های خاص را در یک دایره پیدا می کنید؟

بخش های ویژه در یک دایره E. قضیه 10.15 - AC x = AE x. L. A. 8.9 = BE. بخش هایی که خارج از دایره متقاطع می شوند. معیارهای پاره هایی را پیدا کنید که بیرون و داخل دایره را قطع می کنند. E. قضیه 10.16.. م. هنگامی که دو آکورد در داخل یک دایره قطع می شوند، هر وتر به دو بخش تقسیم می شود که به آنها قطعه وتر می گویند. E
