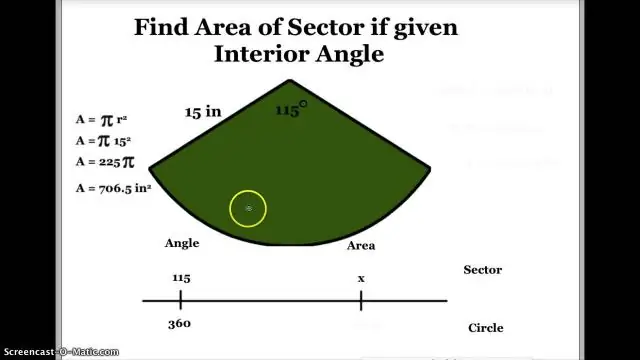
چگونه می توان زاویه یک بخش را در نمودار دایره ای پیدا کرد؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35

1 پاسخ

1. در هر بخش ، 3 بخش وجود دارد که باید در نظر گرفته شود:
2. طول قوس کسری از محیط است بخش مساحت کسری از کل منطقه است. را گوشه کسری از 360 درجه است
3. اگر بخش 20 درصد است نمودار دایره ای ، هر یک از این قسمت ها 20 درصد کل است.
4. 20%×360°
5. 20100×360=72°

به این ترتیب، چگونه درجه یک بخش از یک دایره را پیدا می کنید؟

توضیح: اگر زاویه مرکزی 60 باشد درجه ، مجموع 360 را تقسیم کنید درجه در دایره در 60. این را در اندازه قوس مربوطه ضرب کنید پیدا کردن دور کل دایره . از دور استفاده کنید تا پیدا کردن theradius، سپس از شعاع استفاده کنید پیدا کردن محوطه.

پس از آن، سوال این است که زاویه مرکزی در نمودار دایره ای چیست؟ در یک نمودار دایره ای مشاهدات یا مؤلفه های مختلف با بخش های یک دایره نشان داده می شوند و کل دایره مجموع مقادیر همه مؤلفه ها را نشان می دهد. زاویه مرکزی برای یک جزء به وسیله: گوشه مرکزی برای یک جزء = مقدار مؤلفه مجموع مقادیر همه مؤلفه ها × 360 درجه

به همین ترتیب، چگونه درجه یک درصد را پیدا می کنید؟

یک دایره 360 دارد درجه ، بنابراین اگر می خواهید یک زاویه را بر حسب a بیان کنید درصد ، فقط اندازه گیری زاویه را تقسیم کنید (در درجه ) را در 360 ضرب کنید و در 100 ضرب کنید. برعکس، عدد را تقسیم کنید درصد در 100 و ضرب در 360.

فرمول پیدا کردن زاویه مرکزی چیست؟

فرمول برای S=rθ تصویر زیر رابطه بین شعاع و شعاع را نشان می دهد زاویه مرکزی در رادیان فرمول S=rθ است که در آن s نشان دهنده طول قوس است، S=rθ نشان دهنده the است زاویه مرکزی بر حسب رادیان و r طول شعاع است.