فهرست مطالب:

تصویری: چگونه می توان ویژگی های یک دایره را پیدا کرد؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
ویژگی های دایره
این حلقه ها اگر شعاع مساوی داشته باشند به آنها همگن گفته می شود. قطر a دایره طولانی ترین وتر a است دایره . آکورد مساوی و مساوی حلقه ها دارای محیط مساوی شعاع عمود بر وتر کشیده شده وتر را نصف می کند.
مردم همچنین می پرسند ویژگی های دایره چیست؟
سه مورد از مهمترین خواص به یاد داشته باشید که محیط، که فاصله دور شکل است. قطر، که فاصله از یک سر است دایره به گذرگاه دیگر از مرکز. و شعاع که نصف قطر است.
به همین ترتیب، اجزای دایره و تعریف آن چیست؟ مهم قطعات دایره شعاع: فاصله از مرکز دایره به آن لبه بیرونی وتر: پاره خطی که نقاط انتهایی آن روی a قرار دارند دایره . قطر: وتری که از مرکز می گذرد دایره . طول یک قطر دو برابر طول یک شعاع است.
به همین ترتیب، 8 قضیه دایره چیست؟
یادداشت فنی
- قضیه دایره اول - زاویه در مرکز و در محیط.
- قضیه دایره دوم - زاویه در یک نیم دایره.
- قضیه دایره سوم - زوایا در همان پاره.
- قضیه دایره چهارم - زوایا در چهارضلعی حلقوی.
- قضیه دایره پنجم - طول مماس ها.
چه چیزی دایره نامیده می شود؟
دایره مکان نقاطی است که از یک نقطه معین فاصله دارند، مرکز آن دایره . آ دایره یک شکل صفحه است که توسط یک خط وجود دارد، که نامیده می شود محیط، و به گونه ای است که تمام خطوط مستقیمی که از یک نقطه معین در شکل به محیط کشیده شده اند، با یکدیگر برابر هستند.
توصیه شده:
چگونه می توان محیط دقیق دایره را پیدا کرد؟

محیط = π x قطر دایره (ضریب پی در قطر دایره). به سادگی محیط را بر π و طول قطر را خواهید داشت. قطر فقط شعاع دو است، پس قطر را بر دو تقسیم کنید و شعاع دایره را خواهید داشت
چگونه می توان زاویه یک بخش را در نمودار دایره ای پیدا کرد؟
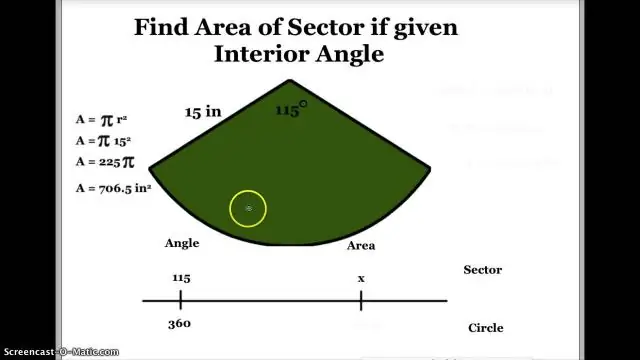
1 پاسخ در هر بخش، 3 قسمت وجود دارد که باید در نظر گرفته شود: طول قوس کسری از محیط است. مساحت این بخش کسری از کل مساحت است. این زاویه کسری از 360 درجه است اگر بخش 20٪ نمودار دایره ای باشد، هر یک از این قسمت ها 20٪ از کل است. 20% × 360 درجه 20100 × 360 = 72 درجه
مماس زاویه روی دایره واحد را چگونه می توان پیدا کرد؟

دایره واحد دارای زوایای مختلفی است که هر یک نقطه مربوط به دایره را دارند. مختصات هر نقطه راهی برای یافتن مماس هر زاویه به ما می دهد. مماس یک زاویه برابر است با مختصات y تقسیم بر مختصات x
چگونه می توان مساحت و حجم دایره را پیدا کرد؟

مساحت سطح = (2 • π • r²) + (2 • π • r • ارتفاع) جایی که (2 • π • r²) مساحت سطح "انتها" و (2 • π • r • ارتفاع است. ) ناحیه جانبی است (مساحت "سمت")
چگونه می توان مرکز دایره را در قسمت مخروطی پیدا کرد؟

مقدار r "شعاع" دایره و نقطه (h، k) "مرکز" دایره نامیده می شود. (h، k) = (0، 0)، سپس معادله به x2 + y2 = r2 ساده می شود
