
تصویری: مشتق Sinh 2x چیست؟
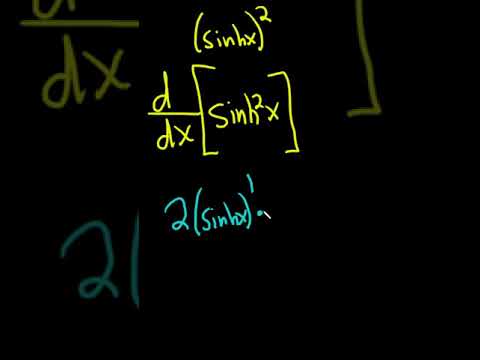
2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
این مشتق سین (u) گناه (u) با توجه به u u cosh(u) cosh (u) است. تمام رخدادهای u u را با 2x2x جایگزین کنید.
به همین ترتیب مردم می پرسند مشتق سینه چیست؟
بنابراین مشتقات از هذلولی سینوسی و هذلولی توابع کسینوس توسط. ( گناه x)'=(ex−e−x2)'=ex+e−x2=coshx, (coshx)'=(ex+e−x2)'=ex−e−x2= گناه ایکس.
همچنین ممکن است سوال شود که مشتق سینوس هایپربولیک چیست؟ توابع هذلولی
| عملکرد | مشتق | نمودار |
|---|---|---|
| cosh(x) | sinh (x) | ↓ |
| tanh (x) | 1-tanh(x)² | ↓ |
| تخت (x) | 1-coth(x)² | ↓ |
| sech (x) | -sech(x)*tanh(x) | ↓ |
با توجه به این موضوع، Cosh و Sinh را چگونه متمایز می کنید؟
اجازه دهید g(x) = cosh x و h(x) = گناه ایکس 2، تابع f ضریب توابع g و h است: f(x) = g(x) / h(x). از این رو از قانون ضریب، f '(x) = [h(x) g '(x) - g(x) h '(x)] / h(x) استفاده می کنیم. 2، برای پیدا کردن مشتق تابع f.
فرمول Sinhx چیست؟
x = e x − e − x 2 sinh x = dfrac{e^x - e^{-x}}{2} sinhx =2ex−e−x؟ کوش x = e x + e - x 2 cosh x =dfrac{e^x + e^{-x}}{2} coshx=2ex+e−x؟
توصیه شده:
مشتق ضریب چیست؟
قانون QUOTIENT در کلمات، این را می توان به این صورت به خاطر آورد: «مشتق یک ضریب برابر است با مشتق پایین ضربات بالا منهای بالا ضربات مشتق پایین، تقسیم بر مجذور پایین»
مشتق Secx 2 چیست؟

می دانیم که مشتق g(x) = sec x g'(x) = secx tanx است، بنابراین 2sec x را در secx tanx ضرب می کنیم تا پاسخ خود را بدست آوریم. می بینیم که مشتق sec 2 x 2sec 2 x tan x است
نمونه ای از یک ویژگی مشتق شده مشترک پستانداران چیست؟

آپومورفی - یک صفت مشتق شده که در اجداد یافت نمی شود اما در گونه های نسلی، به عنوان مثال، ناخن در نخستی ها وجود دارد. اوتاپومورفی - یک ویژگی مشتق شده منحصر به فرد موجود در گونه های عضو یک درجه خاص، به عنوان مثال، فقدان دم در میمون ها
رابطه انتگرال و مشتق چیست؟

مشتق می تواند یک مقدار لحظه ای دقیق برای آن نرخ تغییر به شما بدهد و به مدل سازی دقیق کمیت مورد نظر منجر شود. انتگرال یک تابع را می توان از نظر هندسی به صورت مساحت زیر منحنی تابع ریاضی f(x) که به صورت تابعی از x رسم شده است تفسیر کرد
مشتق حرکت زاویه ای چیست؟

معادلات کلیدی سرعت مرکز جرم جسم غلتان vCM=Rω مشتق تکانه زاویه ای برابر است با گشتاور d→ldt=∑→τ تکانه زاویه ای سیستمی از ذرات →L=→l1+→l2+⋯+→lN برای سیستمی از ذرات، مشتق تکانه زاویه ای برابر است با گشتاور d→Ldt=∑→τ تکانه زاویه ای یک جسم صلب در حال چرخش L=Iω
