فهرست مطالب:

تصویری: چگونه می توان فضای داخلی یک زاویه را پیدا کرد؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
نحوه پیدا کردن زوایای داخلی
- مجموع زاویه در یک مثلث همیشه برابر با 180 درجه است.
- مربع ها 4 ضلع مساوی دارند و مجموع آنها زاویه همیشه برابر با 360 درجه است.
- برای یافتن اندازه گیری زوایای داخلی در یک مربع، مجموع را تقسیم می کنید زاویه (360o) به تعداد اضلاع (4).
به همین ترتیب، پرسیده می شود که چگونه زوایای داخلی و خارجی را پیدا می کنید؟
را فرمول برای محاسبه اندازه یک زاویه داخلی است: زاویه داخلی از یک چند ضلعی = مجموع زوایای داخلی ÷ تعداد اضلاع مجموع زوایای بیرونی یک چند ضلعی 360 درجه است. را فرمول برای محاسبه اندازه یک زاویه بیرونی است: زاویه بیرونی یک چند ضلعی = 360 ÷ تعداد اضلاع.
پس از آن، سوال این است که زاویه راست داخلی چیست؟ طبق تعریف، همه زوایای داخلی از یک مربع هستند زوایای راست -- یعنی همه آنها 90 درجه هستند.
با توجه به این موضوع، نمای داخلی و خارجی یک زاویه چیست؟
به طور خلاصه، ما آموختیم که یک زاویه داخلی هست یک زاویه در داخل یک شکل، در حالی که یک زاویه بیرونی هست یک زاویه از کنار یک شکل و خطی که از سمت مجاور بیرون کشیده شده است. مجموع زوایای داخلی یک مثلث همیشه 180 است.
فرمول زاویه داخلی چیست؟
یک زاویه داخلی در مرز یک چند ضلعی قرار دارد. مجموع همه زوایای داخلی را می توان با استفاده از فرمول S = (n - 2) * 180. همچنین می توان اندازه هر یک را محاسبه کرد زاویه اگر چند ضلعی با تقسیم مجموع بر تعداد اضلاع منظم باشد.
توصیه شده:
چگونه می توان سرعت متوسط را با دو سرعت پیدا کرد؟
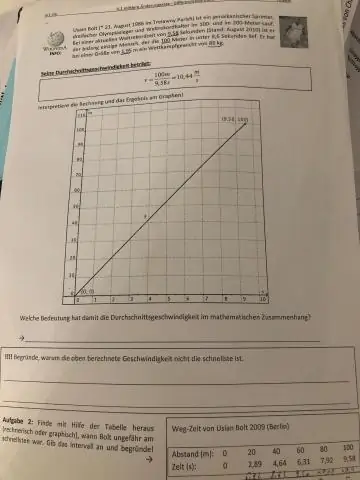
برای بدست آوردن میانگین، مجموع سرعت اولیه و نهایی بر 2 تقسیم می شود. ماشین حساب سرعت متوسط از فرمولی استفاده می کند که نشان می دهد سرعت متوسط (v) برابر با مجموع سرعت نهایی (v) و سرعت اولیه (u) تقسیم بر 2 است
چگونه عبارت زوایای داخلی متناوب موقعیت دو زاویه را توصیف می کند؟

زوایای داخلی متناوب توسط یک متقاطع عرضی دو خط موازی تشکیل می شوند. آنها بین دو خط موازی اما در طرف مقابل عرضی قرار دارند و دو جفت (چهار زاویه کلی) از زاویه های داخلی متناوب را ایجاد می کنند. زوایای داخلی متناوب متجانس هستند، به این معنی که اندازه آنها برابر است
چگونه می توان تغییر انرژی داخلی گاز را پیدا کرد؟

تغییر انرژی داخلی گاز در حجم ثابت. طبق قانون اول ترمودینامیک، u=q+w، جایی که u در انرژی داخلی تغییر میکند، q گرما آزاد میشود و w کار انجام شده در این فرآیند است. اکنون در حجم ثابت، w=0، بنابراین u=q
چگونه می توان زاویه یک بخش را در نمودار دایره ای پیدا کرد؟
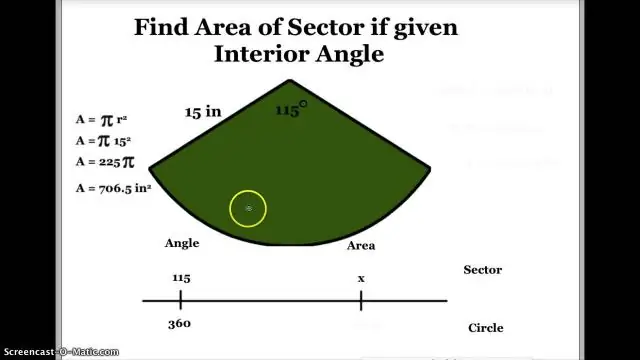
1 پاسخ در هر بخش، 3 قسمت وجود دارد که باید در نظر گرفته شود: طول قوس کسری از محیط است. مساحت این بخش کسری از کل مساحت است. این زاویه کسری از 360 درجه است اگر بخش 20٪ نمودار دایره ای باشد، هر یک از این قسمت ها 20٪ از کل است. 20% × 360 درجه 20100 × 360 = 72 درجه
مماس زاویه روی دایره واحد را چگونه می توان پیدا کرد؟

دایره واحد دارای زوایای مختلفی است که هر یک نقطه مربوط به دایره را دارند. مختصات هر نقطه راهی برای یافتن مماس هر زاویه به ما می دهد. مماس یک زاویه برابر است با مختصات y تقسیم بر مختصات x
