
تصویری: آیا یک تابع از آزمون خط عمودی عبور می کند؟
2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
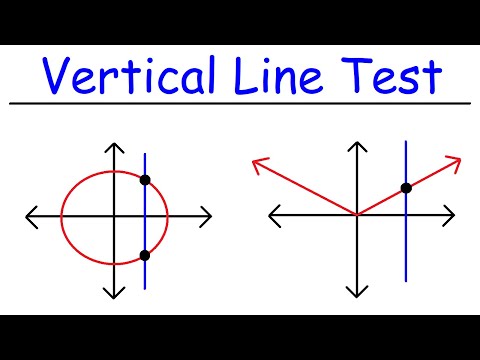
بنابراین معامله اینجاست! اگر یک خط عمودی نمودار را در همه مکان ها دقیقاً در یک نقطه قطع می کند، سپس رابطه a است عملکرد . در اینجا چند نمونه از روابط که همچنین هستند کارکرد چون آن ها قبولی در آزمون خط عمودی.
بنابراین، چگونه متوجه می شوید که آیا یک تابع از آزمون خط عمودی عبور کرده است؟
برای استفاده از تست خط عمودی ، یک خط کش یا لبه مستقیم دیگر بردارید و a را بکشید خط موازی با محور y برای هر مقدار انتخاب شده از x. اگر را خط عمودی شما ترسیم کردید، نمودار را بیش از یک بار برای هر مقدار x قطع می کند، سپس نمودار، نمودار یک نمودار نیست. عملکرد.
قبولی در آزمون خط عمودی به چه معناست؟ توابع نمی توانند بیش از یک مقدار y برای هر مقدار x داشته باشند. اگر یک خط عمودی عبور می کند از طریق یک نمودار بیش از یک بار، آن را به معنای که آن مقدار x بیش از یک مقدار y دارد، بنابراین نمودار نمی تواند به یک تابع مرتبط شود. چیست تست خط عمودی ?
با در نظر گرفتن این، آیا این یک تست خط عمودی تابع است؟
برای اینکه یک رابطه یک باشد عملکرد ، استفاده کنید تست خط عمودی : الف را بکشید خط عمودی در هر نقطه از نمودار، و اگر هرگز بیش از یک بار به نمودار برخورد نکرد، یک است عملکرد . اگر شما خط عمودی دو بار یا بیشتر ضربه می زند، این یک نیست عملکرد.
کدام نمودار از آزمون خط عمودی عبور می کند؟
اگر شما یک خط عمودی در هر نقطه از یکی از نمودارها ، فقط باید عبور از طریق یک نقطه به عنوان مثال، یک مستقیم معمولی خط تقریبا همیشه آزمون خط عمودی را پشت سر می گذارد . اگر سهمی جانبی باشد، نمی شود.
توصیه شده:
آیا نور مرئی از جو زمین عبور می کند؟
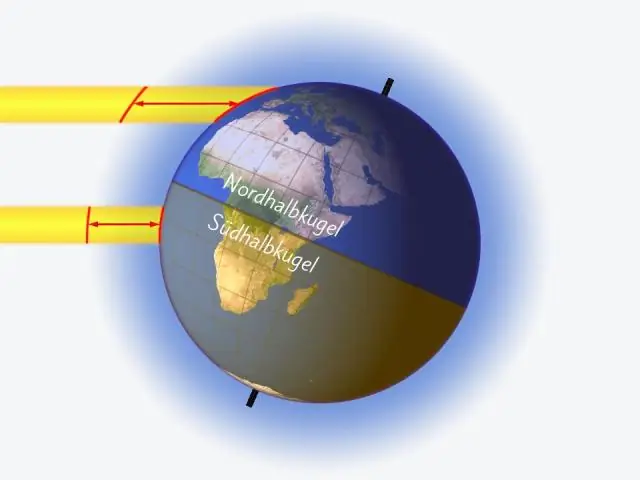
تمام نور مرئی در جو نفوذ می کند، بیشتر نور رادیویی در جو نفوذ می کند و مقداری نور IR از جو عبور می کند. در مقابل، جو ما مانع از رسیدن بیشتر اشعه ماوراء بنفش (UV) و تمام پرتوهای ایکس و گاما به سطح زمین می شود
چگونه یک تابع خطی را به صورت عمودی کوچک می کنیم؟
چگونه: با توجه به معادله یک تابع خطی، از تبدیل ها برای رسم نمودار تابع خطی به شکل f(x)=mx+b f (x) = m x + b استفاده کنید. نمودار f(x)=x f (x) = x. نمودار را به صورت عمودی کشیده یا با ضریب |m فشرده کنید
کدام نمودار در آزمون خط عمودی مردود می شود؟
اگر یک خط عمودی نمودار را در برخی نقاط در بیش از یک نقطه قطع کند، آن رابطه یک تابع نیست. در اینجا چند نمونه از روابطی وجود دارد که توابع نیستند زیرا در آزمون خط عمودی شکست خورده اند
تفاوت بین آزمون t زوجی و آزمون t 2 نمونه چیست؟

از آزمون t دو نمونه ای زمانی استفاده می شود که داده های دو نمونه از نظر آماری مستقل باشند، در حالی که از آزمون t زوجی زمانی استفاده می شود که داده ها به صورت جفت های همسان باشند. برای استفاده از آزمون t دو نمونه ای، باید فرض کنیم که داده های هر دو نمونه به طور نرمال توزیع شده اند و واریانس های یکسانی دارند
آیا آزمون انتگرال می تواند واگرایی را اثبات کند؟

مثال 1 همگرا یا واگرا بودن سری زیر را مشخص کنید. این تابع به وضوح مثبت است و اگر x x را بزرگتر کنیم مخرج بزرگتر می شود و بنابراین تابع نیز کاهش می یابد. انتگرال واگرا است و بنابراین سری نیز با آزمون انتگرال واگرا می شود
