
تصویری: آیا هر دو جفت ضلع مقابل در یک لوزی موازی هستند؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-11-26 05:37
آ لوزی تمام خواص a را دارد متوازی الاضلاع : هر دو جفت طرف مقابل هستند موازی . هر دو جفت طرف مقابل هستند برابر در طول. هر دو جفت مخالف زاویه هستند برابر.
علاوه بر این، آیا هر دو جفت ضلع مقابل در متوازی الاضلاع موازی هستند؟
تعریف: الف متوازی الاضلاع چهار ضلعی است با هر دو جفت ضلع مخالف موازی هستند . قضیه: اگر یک چهارضلعی a باشد متوازی الاضلاع ، دارای 2 ست طرف مقابل متجانس. قضیه: اگر یک چهار ضلعی دارای زوایای متوالی باشد که مکمل یکدیگر هستند، a است متوازی الاضلاع.
به همین ترتیب، چهار ضلعی با یک جفت ضلع مقابل که موازی هستند چیست؟ ذوزنقه ای
علاوه بر این، آیا لوزی دارای اضلاع متضاد موازی است؟
آ لوزی یک شکل صاف است با 4 برابر سر راست طرفین . طرف مقابل هستند موازی ، و مقابل زاویه هستند برابر (متوازی الاضلاع است). و قطرهای "p" و "q" از آ لوزی یکدیگر را در زوایای قائم نصف کنید.
یک لوزی چند ضلع موازی دارد؟
هر لوزی دارد دو مورب جفت رئوس مخالف و دو جفت از اضلاع موازی.
توصیه شده:
آیا o2 و o3 یک جفت ایزوتوپ هستند؟

ایزوتوپ ها موادی هستند که تعداد پروتون یکسانی دارند اما در تعداد نوترون ها با هم تفاوت دارند. بنابراین، جفت ایزوتوپ بالا باید از یک عنصر باشند. O2 و O3 در فرمول مولکولی متفاوت هستند، اما همچنان از یک نوع اتم ساخته شده اند، بنابراین آنها آلوتروپ هستند، در حالی که 32S و 32S2- ایزوتوپ نیستند
چه چهار ضلعی ها دارای ضلع های مخالف موازی هستند؟

چهار ضلعی با خطوط ضلع مقابل موازی به عنوان متوازی الاضلاع شناخته می شود. اگر فقط یک جفت ضلع مخالف لازم باشد که موازی باشند، شکل یک ذوزنقه است. ذوزنقه ای که طول اضلاع غیر موازی آن برابر است، متساوی الساقین نامیده می شود
چهار ضلعی با 2 ضلع موازی چیست؟

چهارضلعی با دو جفت ضلع موازی را متوازی الاضلاع می گویند. اگر این جفت ضلع های موازی در زوایای قائم به یکدیگر برسند متوازی الاضلاع نیز یک مستطیل است
اگر هر جفت ضلع موازی باشند کدام کدام است؟

اگر یک جفت ضلع مقابل یک چهار ضلعی موازی و همسو باشند، آن چهارضلعی متوازی الاضلاع است. اگر هر دو جفت زوایای متضاد یک چهار ضلعی همسو باشند، آن چهارضلعی متوازی الاضلاع است
چگونه ضلع مقابل مثلث را با استفاده از فیثاغورث پیدا کنید؟
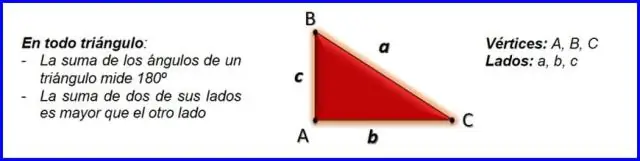
مثلث های قائم الزاویه و قضیه فیثاغورث قضیه فیثاغورث، a2+b2=c2، a 2 + b 2 = c 2، می تواند برای یافتن طول هر ضلع یک مثلث قائم الزاویه استفاده شود. ضلع مقابل زاویه قائمه را هیپوتنوز می نامند (ضلع c در شکل)
