
تصویری: آیا یک ماتریس شبیه معکوس آن است؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
فقط به یک 2x2 فکر کنید ماتریس به این معنا که مشابه معکوس آن بدون اینکه ورودی های مورب 1 یا -1 باشند. مورب ماتریس ها انجام خواهد داد. بنابراین، A و معکوس از A هستند مشابه ، بنابراین مقادیر ویژه آنها یکسان است. اگر یکی از مقادیر ویژه A n باشد، مقادیر ویژه ای از معکوس آن 1/n خواهد بود.
همچنین پرسیده شد که آیا یک ماتریس شبیه به جابجایی آن است؟
هر مربع ماتریس بیش از یک میدان است شبیه به جابجایی آن و هر مجموعه مربعی ماتریس است مشابه به یک مجتمع متقارن ماتریس.
به همین ترتیب، آیا همه ماتریس های معکوس شبیه هم هستند؟ اگر A و B هستند مشابه و معکوس پذیر ، سپس A-1 و B-1 هستند مشابه . اثبات از آنجا که همه را ماتریس ها هستند معکوس پذیر ، می توانیم معکوس هر دو طرف را بگیریم: B–1 = (P–1AP)–1 = P–1A–1(P–1)–1 = P–1A–1P، بنابراین A–1 و B–1 هستند مشابه . اگر A و B هستند مشابه ، Ak و Bk برای هر k = 1, 2,.
با توجه به این موضوع، آیا یک ماتریس می تواند مشابه خودش باشد؟
یعنی هر ماتریس است شبیه خودش : I−1AI=A. اگر A باشد مشابه به B، سپس B است مشابه به A: اگر B=P−1AP، آنگاه A=PBP−1=(P−1)−1BP−1. اگر A باشد مشابه به B از طریق B=P−1AP، و C است مشابه به B از طریق C=Q−1BQ، سپس A است مشابه به C: C=Q−1P−1APQ=(PQ)-1APQ.
اگر ماتریس ها شبیه هم باشند به چه معناست؟
در جبر خطی دو n در n ماتریس ها A و B نامیده می شوند مشابه اگر یک n-by-n وارونه وجود دارد ماتریس P طوری که. ماتریس های مشابه نقشه خطی یکسانی را تحت دو (احتمالا) پایه متفاوت نشان می دهد که P تغییر پایه است ماتریس.
توصیه شده:
چگونه می توان یک ماتریس را به یک ماتریس هویت تبدیل کرد؟

ویدئو علاوه بر این، چگونه معکوس یک ماتریس را با استفاده از یک ماتریس هویت پیدا می کنید؟ به همین ترتیب برای ماتریس ها . اگر a را ضرب کنید ماتریس (مانند الف) و آن معکوس (در این مورد، A – 1 )، شما دریافت می کنید ماتریس هویت I. و نکته از ماتریس هویت این است که IX = X برای هر کدام ماتریس X (به معنی "
چگونه معکوس افزودنی یک ماتریس را پیدا می کنید؟

برای بدست آوردن معکوس افزودنی ماتریس داده شده، فقط باید هر عنصر ماتریس را در -1 ضرب کنیم. وقتی هر عنصر ماتریس را در -1 ضرب کنیم، برابر با -A می شود. بنابراین، A+(-A) برابر 0 می شود که در آن 0 یک ماتریس تهی است. این تعریف اولیه معکوس افزودنی را برآورده می کند
آیا شبیه سازی میتوز است یا میوز؟

تقسیم سلولی از دو طریق می تواند در انسان و اکثر حیوانات دیگر اتفاق بیفتد که میتوز و میوز نامیده می شوند. هنگامی که یک سلول از طریق میتوز تقسیم می شود، دو کلون از خود تولید می کند که هر کدام دارای تعداد کروموزوم یکسانی هستند. هنگامی که یک سلول از طریق میوز تقسیم می شود، چهار سلول به نام گامت تولید می کند
چگونه ثابت کنید که یک ماتریس یک زیرفضا است؟

متمرکز کننده یک ماتریس یک زیرفضا است. اجازه دهید V فضای برداری n×n ماتریس و M∈V یک ماتریس ثابت باشد. W={A∈V∣AM=MA} را تعریف کنید. مجموعه W در اینجا مرکز ساز M در V نامیده می شود. ثابت کنید که W زیرفضای V است
آیا شبیه سازی درمانی گران است؟
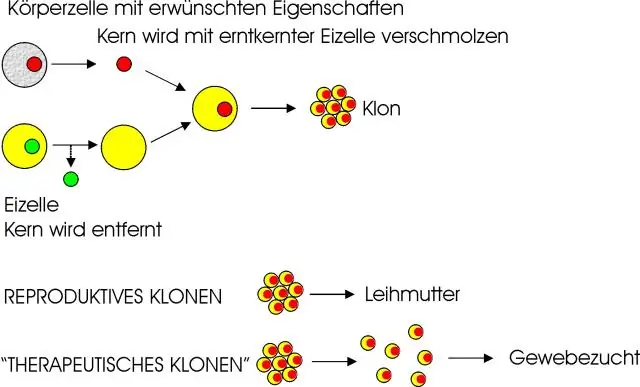
بسیاری از دانشمندان می گویند شبیه سازی درمانی، که به عنوان انتقال هسته ای سلول های سوماتیک نیز شناخته می شود، راهی برای درمان موفق سلول های بنیادی نخواهد بود. در واقع، اگر شبیهسازی درمانی حیاتی بود، درمان با سلولهای بنیادی را بسیار گران میکرد. این بدان معنا نیست که شبیه سازی درمانی کاملاً بی فایده است
