فهرست مطالب:

تصویری: چگونه بادبادک را در هندسه مختصات اثبات می کنید؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
در اینجا دو روش وجود دارد:
- اگر دو جفت ناهمگون از ضلع های متوالی یک چهار ضلعی همگن باشند، این یک بادبادک (معکوس از بادبادک تعریف).
- اگر یکی از قطرهای یک چهار ضلعی عمود بر دیگری باشد، این یک بادبادک (مقابل یک ملک).
متعاقباً ممکن است این سؤال نیز مطرح شود که بادبادک چه ویژگی هایی دارد؟
بادبادک ویژگی ها شامل (1) دو جفت ضلع متوالی و متجانس، (2) زوایای غیر رأس متجانس و (3) مورب های عمود بر هم هستند. سایر خصوصیات مهم چند ضلعی که باید با آنها آشنا شد عبارتند از خواص ذوزنقه، خواص متوازی الاضلاع، خواص لوزی، و خواص مستطیل و مربع.
همچنین بدانید آیا مستطیل عمود بر هم است؟ همانطور که از تصاویر سمت چپ مشاهده می کنید، مورب های a مستطیل در زاویه قائمه همدیگر را قطع نمی کنند (اینطور نیستند عمود بر ). (مگر اینکه مستطیل یک مربع است.) و زوایای تشکیل شده توسط تقاطع همیشه یک اندازه (اندازه) نیستند. زوایای مرکزی مقابل هم اندازه هستند (همخوان هستند.)
پس از آن، سوال این است که آیا بادبادک عمود است؟
تعریف: الف بادبادک چهار ضلعی است که چهار ضلع آن به گونه ای ترسیم شده است که دو مجموعه مجزا از همدیگر وجود دارد، متجانس طرفین قضیه: اگر یک چهار ضلعی بادبادک است ، مورب ها هستند عمود بر . قضیه: اگر یک چهار ضلعی بادبادک است ، دارای یک جفت زاویه مخالف است متجانس.
آیا مستطیل متوازی الاضلاع است؟
آ مستطیل دارای دو جفت ضلع مخالف موازی و چهار زاویه قائمه است. همچنین یک است متوازی الاضلاع ، زیرا دارای دو جفت ضلع موازی است.
توصیه شده:
چگونه قانون اعداد بزرگ را اثبات می کنید؟

ویدیو همچنین بدانید، چگونه قانون اعداد بزرگ را توضیح می دهید؟ این قانون اعداد بزرگ بیان می کند که یک میانگین نمونه مشاهده شده از a بزرگ نمونه نزدیک به میانگین جمعیت واقعی خواهد بود و هر چه نمونه بزرگتر باشد به آن نزدیکتر می شود. به همین ترتیب، قانون ضعیف اعداد بزرگ چیست؟ این قانون ضعیف اعداد بزرگ که به عنوان قضیه برنولی نیز شناخته می شود، بیان می کند که اگر شما نمونه ای از متغیرهای تصادفی مستقل و توزیع شده یکسان داشته باشید، با بزرگتر شدن حجم نمونه، میانگین نمونه ب
کدام اثبات از ارقام روی صفحه مختصات برای اثبات ویژگی های هندسی استفاده می کند؟

برهانی که از ارقام روی یک صفحه مختصات برای اثبات ویژگی های هندسی استفاده می کند، مثلثاتی نامیده می شود
اثبات مستقیم در هندسه چیست؟

رایج ترین شکل اثبات در هندسه اثبات مستقیم است. در یک اثبات مستقیم، نتیجه ای که باید اثبات شود به طور مستقیم در نتیجه سایر شرایط موقعیت درست نشان داده می شود. اگر گزاره شرطی istrue، که می دانیم آن است، آنگاه q، گزاره بعدی در اثبات نیز باید درست باشد
چگونه می توان یک صفحه مختصات را در هندسه ساخت؟
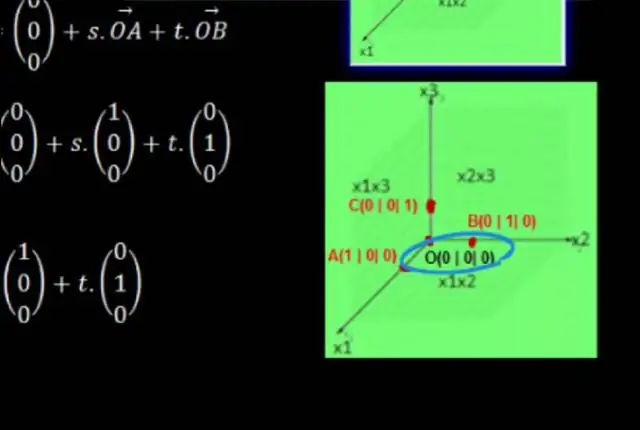
برای ایجاد یک صفحه مختصات، مراحل زیر را دنبال می کنیم: دو خط عددی عمود بر یکدیگر بکشید که در نقطه 0 در هر دو خط قطع می شوند. خط اعداد افقی را به عنوان محور x و خط اعداد عمودی را به عنوان محور y برچسب گذاری کنید
چگونه قانون رائول را اثبات می کنید؟

قانون رائول را برای املاح غیر فرار در حلال فرار بیان و اثبات کنید. همچنین هر دو محدودیت قانون رائول را ذکر کنید. فشار بخار محلول یک املاح غیر فرار برابر است با فشار بخار حلال خالص در آن دما ضرب در کسر مولی آن
