
تصویری: چگونه قضیه کوچک فرما را انجام می دهید؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
قضیه کوچک فرما بیان می کند که اگر p یک عدد اول باشد، برای هر عدد صحیح a، عدد a است پ - a مضرب صحیح p است. آپ ≡ a (mod p). حالت خاص: اگر a بر p بخش پذیر نباشد، قضیه کوچک فرما معادل این جمله است که الف پ-1-1 مضرب صحیح p است.
به این ترتیب، چگونه قضیه کوچک فرما را اثبات می کنید؟
فرض کنید p یک عدد اول و یک عدد صحیح باشد، سپس aپ = a (mod p). اثبات اگر p a را تقسیم کند، نتیجه سه گانه است (هر دو طرف صفر هستند). اگر p a را تقسیم نکند، فقط باید همخوانی را در آن ضرب کنیم قضیه کوچک فرما توسط a برای تکمیل اثبات.
همچنین بدانید که راه حل آخرین قضیه فرما چیست؟ راه حل برای آخرین قضیه فرما . آخرین قضیه فرما (FLT)، (1637)، بیان می کند که اگر n یک عدد صحیح بزرگتر از 2 باشد، در آن صورت یافتن سه عدد طبیعی x، y و z غیرممکن است که در آن برابری برآورده شود که (x، y)> 0 در xn+yn باشد. =zn.
با توجه به این موضوع، چرا قضیه کوچک فرما مهم است؟
قضیه کوچک فرما اساسی است قضیه در نظریه اعداد ابتدایی، که به محاسبه توان اعداد صحیح و مدول اعداد اول کمک می کند. این یک مورد خاص از اویلر است قضیه ، و است مهم در کاربردهای نظریه اعداد ابتدایی، از جمله آزمایش اولیه و رمزنگاری کلید عمومی.
منظور از قضیه اویلر چیست؟
قضیه اویلر . تعمیم فرما قضیه شناخته شده است قضیه اویلر . به طور کلی، قضیه اویلر بیان می کند که، "اگر p و q نسبتا اول باشند، " که در آن φ است اویلر تابع totient برای اعداد صحیح یعنی تعداد اعداد غیر منفی که کوچکتر از q و نسبتاً اول به q هستند.
توصیه شده:
چگونه تست دوربین واتسون را در Minitab انجام می دهید؟
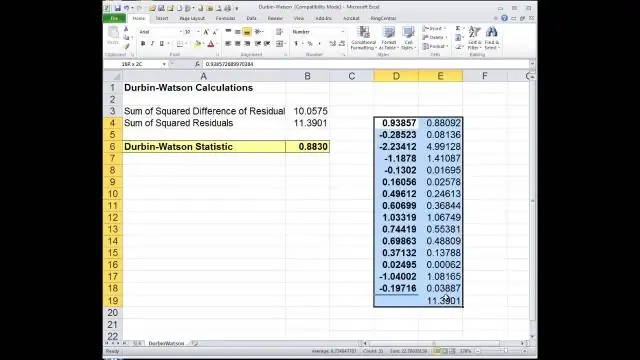
در Minitab: روی Stat > Regression > Regression > Fit Regression Model کلیک کنید. روی «نتایج» کلیک کنید و آمار دوربین واتسون را بررسی کنید
چگونه مشکلات کلمه سیستم معادلات را انجام می دهید؟

برای حل یک سیستم معادله مسائل کلمه، ابتدا متغیرها را تعریف کرده و سپس معادلات را از کلمه مسائل استخراج می کنیم. سپس میتوانیم سیستم را با استفاده از روشهای نمودار، حذف یا جایگزینی حل کنیم
چگونه بهترین فوران آتشفشانی را انجام می دهید؟

لیوان پلاستیکی جوش شیرین و سرکه آتشفشانی (ما یک بطری آب را امتحان کردیم، اما لیوان پلاستیکی خیلی بهتر عمل کرد) آب. حداقل 3-4 قاشق غذاخوری جوش شیرین (معمولاً 4-6 قاشق غذاخوری که باعث کف زیاد آن می شود و 2-3 فوران می کند) 1 قاشق چایخوری صابون ظرفشویی. 1/2 اونس تا 2 اونس رنگ قابل شستشو بسته به شدت رنگ مورد نظر
چگونه رویدادهای مرکب احتمال را انجام می دهید؟
تعیین احتمال یک رویداد مرکب شامل یافتن مجموع احتمالات رویدادهای منفرد و در صورت لزوم حذف هر گونه احتمال همپوشانی است. یک رویداد ترکیبی انحصاری رویدادی است که در آن رویدادهای متعدد با هم همپوشانی ندارند. در اصطلاح ریاضی: P(C) = P(A) + P(B)
چگونه یک تستر تداوم ساده انجام می دهید؟

ویدیو همچنین سوال این است که تستر تداوم ساده چیست؟ آ تستر تداوم هست یک ساده دستگاهی متشکل از دو کاوشگر تست و نشانگر چراغ (LED) یا زنگ. برای تشخیص وجود استفاده می شود تداوم یا شکستگی بین دو سر هادی که به پروب های آزمایش آن متصل است.
