
تصویری: آیا شعاع دایره می تواند صفر باشد؟

2024 نویسنده: Miles Stephen | [email protected]. آخرین اصلاح شده: 2023-12-15 23:35
تا جایی که من می دانم، چیزی در تعریف الف وجود ندارد دایره که مشخص می کند که آن است شعاع نمیتونه باشه صفر … با این حال، الف دایره با شعاع صفر بسیاری از خواص را از دست می دهد حلقه ها . اما الف دایره با یک شعاع از صفر را نمی توان به دیگری مقیاس کرد شعاع.
با در نظر گرفتن این موضوع، دایره ای با شعاع 0 چیست؟
اگر شعاع صفر است، پس واقعاً a نیست دایره ، اما ممکن است منحط خوانده شود دایره --یعنی آنچه را که اگر کمی تعریف a را گسترش دهید به دست می آورید دایره با استفاده از معادله یکسان، اما با ساختن آن را به حد افراط برسانید شعاع صفر
پس از آن، سوال این است که آیا یک دایره می تواند کوچکتر از یک شعاع باشد؟ بله، یک دایره می تواند مثبت داشته باشد شعاع . آ دایره با یک شعاع از کمتر از یکی به اندازه مربعی با طول ضلع بدون مشکل است کمتر از یکی
همچنین بدانید آیا شعاع دایره می تواند منفی باشد؟
آره، شعاع می تواند منفی باشد ، به این معنی که در جهت کاملا مخالف یک سمت مشخص از آن اندازه گیری می شود دایره . اگر شعاع صفر است پس a بیشتر نیست دایره اما یک نکته است
شعاع دایره نقطه ای چقدر است؟
معادله کلی برای a دایره x2+y2+2gx+2fy+c=0 است که h=−g و k=−f است. این شعاع سپس r=√g2+f2−c است. اگر g2+f2−c=0، آنگاه a است دایره نقطه ای . اگر g2+f2−c>0، آنگاه یک واقعی است دایره.
توصیه شده:
آیا یک مولکول غیرقطبی می تواند پیوند هیدروژنی داشته باشد؟

اگر مولکول غیرقطبی باشد، هیچ برهمکنش دوقطبی-دوقطبی یا پیوند هیدروژنی نمی تواند رخ دهد و تنها نیروی بین مولکولی ممکن، نیروی ضعیف واندروالس است
آیا مربع چی می تواند منفی باشد؟
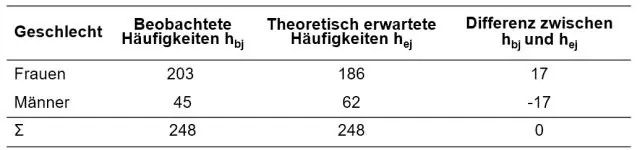
آیا منظورتان این است که آیا مقادیر مجذور کای ممکن است منفی باشند؟ پاسخ خیر است. مقدار مربع کای نمی تواند منفی باشد زیرا بر اساس مجموع اختلافات مجذور (بین نتایج به دست آمده و مورد انتظار) است
آیا ژیروسکوپ می تواند خطای صفر داشته باشد؟

محور عمودی ژیروسکوپ تمایل دارد خود را با عمودی ظاهری هماهنگ کند. در مسیرهای شمالی یا جنوبی و در مسیرهای شرقی یا غربی، قطب نما به طور مساوی روی هر دو طرف قرار می گیرد و خطای حاصل صفر است. اگر این اتفاق بیفتد، خطای ژیروسکوپی نامیده می شود زیرا به شمال واقعی اشاره نمی کند
تفاوت بین شعاع و شعاع انحنا چیست؟

شعاع انحنا شعاع دایره ای است که در نقطه معینی منحنی را لمس می کند و در آن نقطه مماس و انحنای یکسان دارد. شعاع فاصله بین مرکز و هر نقطه دیگر در محیط دایره یا سطح کره است. در حلقه ها باید از عبارت شعاع استفاده کنید
آیا این درست است که هر قطر یک دایره نصف شعاع آن است؟

خیر، قطر یک دایره دو برابر شعاع آن است
